Grothendieck topology

　PDF｜Grothendieck位相｜

　Grothendieck topologyとは通常位相空間論で扱う、開集合の族という意味の位相ではなく、その一般化である。彼は集合とその部分集合族、という形ではなくcategoryとfunctorの言葉で位相を記述しようとした。その根底にあるのは空間の位相というものから、category(poset)が構成できるというところだとは思う。
　彼はまず空間の開集合というのはその空間へのinclusionという特別なmorphismだけを見ているという点に気づいた。だが、代数多様体などでZariski topologyを考えた場合、そこに現れる開集合は非常に少なくて議論がしにくいという問題を抱えていた。そこで発想を変えて、空間へのすべてのmorphismを開集合と考えれば開集合は否応なしに増える。まぁ、それだと無尽蔵に増えすぎるのでGrothendieckが考えたのはe'tale（local homeomorphism）というcovering mapのようなものを考えた。もちろん開集合からのinclusionというのもこれに含まれる。

　Cをcategoryとしたとき、そのobjectであるXに対し、X上のsieveというものを、CのtergetがXであるmorphismの族で任意のmorphismの前からの合成に対し、閉じているものとする。これは、なんとなく環におけるidealのようにも感じる。別の言い方をすれば、Yoneda embeddingを考えたとき、

　　　　　　　　　　　　

h(X) : C^op → Setのsubfunctorの集合がちょうどX上のsieveのSieve(X)と同型である。
　Cのobjectから、sieveを全て集め、そのpower setへの写像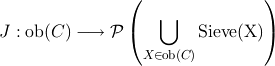

　　　　　　　　　

が様々な条件を満たすとき、JをCのGrothendieck topologyと呼び、(C,J)の組をGrothendieck siteと呼ぶ。この条件については、位相空間の場合と照らし合わせていないとその意味は見えずらい。なので位相空間Xに対し、そのtopologyからなるposetをTと書くと、TのobjectはXの開集合であり、

　　　　　　　　　

で定義すれば、これがgrothendieck topologyとなる。これが一番の例である。

　Grothendieck site上ではpresheafから、張り合わせの条件を入れる事によりsheafを考える事ができる。そのhomologyやcohomologyなんかもGrothendieckは考えていたようだ。このsheafのcategoryはGrothendieck toposと呼ばれたりもする。
　Sheafのより高次元のversionとしてstackが考えられるが、これもGrothendieck位相の被覆に関する張り合わせ条件で定義される。

　Grothendieck topologyには同値な条件としてcovering axiomなど多数ある。【KS05】や、【MM92】なんかを見ると良いかもしれない。あとは、【Vis04】なんかもある。